Bir olasılık, bir şeylerin nasıl olabileceği hakkında yürütülen tahminlerdir ve olasılık fikri şansı incelemekle ilgilidir. Bir olayın nasıl olabileceğini ya da olamayacağını belirleyen, matematiğin bir parçasıdır. Olasılık, sadece bir rehber tahmin olduğundan dolayı bir şeyin olacağını garanti etmemektedir. Bozuk para atmak ve zar atmak en yaygın örneklerden ikisidir. Olasılığın farklı türleri vardır ve aşağıda temek olasılık türleri hakkında bilgiler bulunmaktadır.
Klasik Olasılık
Bu çok yaygın bir olasılık türüdür ve en kolay şekilde bir zar atarak veya havaya bir para atarak ne olacağını göz önünde bulundurarak gösterilebilir. Bir hakem bir futbol maçının başlangıcında bir para atarsa ve sahaya inerse, sadece iki olasılık ortaya çıkar, kale seçimi ve ilk vuruşun kimde olacağı gibi. Belli bir tarafa düşme olasılığı, muhtemel sonuçların tümü (bu durumda, sadece iki) belirlenerek ve daha sonra, o para her atıldığında ne olduğunu kaydederek hesaplanabilir. Başka bir deyişle, yazı tura 10, 20 ya da 50 kez atılabilir, ardından her sonucun ne olduğu yazılabilir ve belirli bir sonucun klasik olasılığının ne olduğu belirlenebilir.
Klasik olasılıkta istatistik içeren her deneyde, her birinin aynı olma şansına sahip olan unsurlar olacağını beyan edilir. Altı kenarı olan bir kalıp yuvarlanırsa olasılık, bir madeni para atma gibi, her seferinde seçimlere yönelik olasılığa yol açacak gibi, altı sayıdan birine inme olasılığı eşittir. Başka bir deyişle olasılık, olası sonuçların sayısına bölünen olumlu sonuçların sayısına eşittir.
Şartlı Olasılık
Bu tür muhtemelen, özünde birbirine bağlı olan bir grup olayı dikkate almaktadır. Normalde daha sonra performansları etkileyen geçmiş performans gibi faktörlere bakar, böylece bu belirli performansın olasılığı belirlenebilir. Başka bir deyişle, tüm resme bakılır ve gelecekte neler olabileceğini belirlemek için geçmişte neler olduğu göz önüne alınır. Koşullu olasılık, delil, varsayım veya iddia ile başka bir olayın gerçekleştiği belirli bir durumun olasılığını ölçer.
Diyelim ki bir kişinin herhangi bir günde, boğaz ağrısına sahip olma olasılığı % 5’tir. Her şey yolunda ve güzel, ama bir kişinin gripten acı çektiğini varsayar ya da bilindiği takdirde, onun da boğaz ağrısına sahip olmasının koşullu ihtimalinin çok daha muhtemel olduğu zaten bilinir. Bu şekilde tarif edilebilir: X’in, XYZ veya P (ABC / XYZ) olarak bilinen koşullar altında meydana gelme olasılığı, burada P’nin olasılıkları, ABC ve XYZ ise iki olaydır. Yukarıdaki örnekte, grip hastası bir kişinin de boğaz ağrısıyla acı çekmesi olasılığı % 75’e kadar çıkabilir.
Deneysel Olasılık
Olan bir şeyin deneysel olasılığı iki şey tarafından belirlenir. İlk olarak, toplam deneme sayısının dikkate alınması gerekir. İkincisi, toplam sonuç sayısı dikkate alınır. Para atıldığında 100 kez yuvarlanırsa ve sonuç 40’ında aynı tercihse teorik olasılık 40/100 ya da 0,4 olacaktır. Bu olasılık, belirli bir sonucun kaç kez yapıldığını, yapılan denemelerin sayısına bölünerek açıklar.
Markov Zinciri Olasılığı
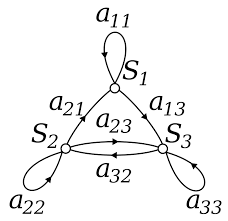Koşullu olasılığa benzerliklerle, bir Markov zinciri olasılığı olayların sırasına ve bu olasılıkların her birinin önceki bir olayda olanlara ve hatta bir olay grubuna bağlı olduğu gerçeğine bakar. Dışarıda kar yağıyorsa ve şu andan bir saat mi yoksa üç saat sonra mı kar yağacağını merak ediliyorsa, tahminini ilk saatte ne kadar kar yağdığına dayandırılabilir.
Markov zinciri olasılığı, olasılıkta daha fazla verimlilik elde etmek için matrisleri kullanır ve belirli hava koşullarından kalıplarının ne kadar iyi performans göstereceğine kadar her şeyin belirlenmesinde kullanılabilir. Her ne tartışılıyorsa, futbol puanları, belirli rakamlar veya harfler olsun, her zaman sınırlı sayıda durum vardır ve mevcut durum 1 (örneğin dışarıda kar yağıyor) ve geçen zaman miktarı 2 (örneğin, bir saat) tarafından daima belirlenir. Markov zinciri olasılıkları her zaman bir dizi geçişten oluşur. Bu geçişler, Markov özelliğini ya da hafızasız olarak bilinen stokastik bir sürecin özelliğini karşılayan olasılık dağılımına göre belirlenir.
Kişisel (Öznel) Olasılık
Bu belki de en az güvenilir olasılıktır, çünkü birinin kişisel yargı ve akıl yürütmesine dayanır. Subjektif veya kişisel olasılıkla, olasılık, bir bireyin olmasını beklediği bir sonuca dayanır. Resmi hesaplamalar veya yorumlar kullanılmaz, ancak olasılık esas olarak bir kişinin konuyla ilgili hislerini ve bilgilerini esas alır. Örneğin, bir kişi bazı arkadaşlarıyla basketbol veya hokey maçı izliyorsa, oyunun başında A Takımının kazanacağını beyan edebilir. Bu varsayım, belirli bir takımın kazanmasını istediğin gerçeğine dayanıyor olabilir, fakat aynı zamanda şu anki sıralamaları gibi şeylere de dayanabilir. Her durumda, öznel olasılık, bazı takımların kazanacağını düşündüğünüz bir ifade oluşturmak için hem temel gerçekleri hem de kişinin öznel görüşlerini içerir.
Göreceli Frekans Yorumlama Olasılığı
Olasılığın göreceli frekans yorumunda, birçok kez belirli bir deney yaparak başlanır ve ardından göreceli frekansı gerçek ölçümlere veya gözlemin kendisine dayandırılır. Örneğin, 50 kez bir kalıbı yuvarlarsa ve dördüncü rakam 15 kez gelirse, dördüncü sayının göreceli frekansı 15/50’dir.
Standart Olasılık
Olasılık her zaman, bu toplam sayı içinde belirli bir sonucun kaç kez olabileceğini gösteren olası sonuçların karşılaştırılmasını içerir. Standart olasılık ile ilk olayın asla ikinci veya üçüncü olayın sonucunu etkilemediği belirli olaylara bakmak zorunda kalınır.
Teorik Olasılık
Bu, gerçekleşen bir şeyin olasılığını belirlemenin en kolay yollarından biridir. Olası XYZ ihtimaline dayanıyor. Bir madalyonun başlarına veya kuyruklarına ineceği teorik olasılığını anlamaya çalışıyorsa, önce sadece bu iki olasılığın ortaya çıkacağı bilinmeniz gerekir. Bir madalyonun fırlatılmasında, sadece iki olasılık vardır, başlangıç ve bitiş. Ve bu nedenle, madalyonun fırlatılmasının teorik olarak başta jeton atmasıyla sonuçlanabileceği teorik olasılığı ikide birdir ve bu da 1: 2 olarak gösterilmiştir. Seçeneklerin sayısını (bu durumda iki) göz önünde bulunduruluyorsa ve bu öncül teorik olasılığa dayandırılır. Madalyonun üç tarafı varsa ve kafaları üç olasılıktan biriyse, bu durumda kafalara iniş üçte bir olasılık veya 1: 3 olacaktır
Teorik olasılıklara bakmanın bir başka yolu, bir şeylerin olma ihtimalinin eşit olduğunu söylemektir. Bir kalıbın altı tarafı vardır ve birini yuvarladığınızda sonucu görebilirsiniz, altı tarafın da eşit görünme şansı olduğunu söylenebilir.
Koşulsuz Olasılık
Bu olasılık türü, tek bir sonucun mümkün olan toplam sonuç örneğinden kaynaklanabileceği tek bağımsız şansını ifade eder. Bir etkinliğin koşulsuz olasılığını bulmak isteniyorsa, o özel etkinliğin sonuçlarının toplamını ekleyebilir ve ardından olası toplam sonuç sayısına bölünür. Bir grup insanı görüntüleniyorsa ve rastgele birini seçiyorsa, bu, o gruptaki her kişinin aynı seçme şansına sahip olduğu anlamına gelir. Bir kadını ya da belirli bir yaş aralığında bir kişiyi seçmeye karar veriliyorsa olasılıklar oldukça doğal olarak biraz farklıdır.
Bazı Olasılık Örnekleri ve İlginç Bilgiler
Terörizm: Bir teröristin bombasının kurbanı olmak, tehlikeli bir asteroit tarafından vurulma ihtimalinden daha düşüktür; Aslında, ikincisi gerçekleşmek için 1.860 kat daha fazladır.
Bozuk para birikimleri: Bozuk para atma olasılıkları genellikle belirli olasılıkların örnekleri olarak kullanılır, ancak zarları 100 kez atıldığında, o zamanların 50’si baştaki seçim, 50 side sonraki ile bitme şansı kabaca % 8’dir.
Bebek dişleri: İşte ilginç bir istatistik her 2.000-3.000 bebekten biri zaten ağzında bir dişle doğmaktadır.
Erkek ve kadınların kanser olma olasılığı: Her ne kadar testis kanseri erkeklerin düşünmesi için korkutucu olsa da gerçek şu ki, testis kanserinden daha meme kanseri ölme olasılığı daha yüksektir ve erkekler de meme kanseri olur.
CPR (kalp masajı) riski: Bir kişi yaşamının bir noktasında CPR almak zorunda kalırsa olaydan üç ay sonra eski haline dönme şansı sadece% 3’tür.
Güneşte çok fazla yanmak: Melanomların yaklaşık% 100’ünün güneş yanığı kaynaklı olmasından dolayı, Avustralya’da yaşayan birinin güneşte çok fazla zaman geçirdiğinden 70 yaşında geldiğinde % 66 oranında kanser yaşama riski vardır
Köpekbalığı saldırısı: Her ne kadar şansınız bir köpekbalığı tarafından saldırıya uğramaktan 11.5 milyonda yalnızca biri olsa da, bu 175 milyon şansı olan bir Powerball yarışmasını kazanmaktan daha muhtemeldir.
Doğum gününde ölüm: İnsanların doğum günlerinde ölme riski yılın diğer 364 gününden daha fazla ölme olasılığı daha yüksektir.
Beyzboll: Yetişkin beyzbol hayranlarından, 9.77’de New York Yankees hayranı olma şansına sahiptir.
Doğum günü paylaşımı: İçinde sadece 60 kişi bulunan bir odada, aynı doğum gününe sahip iki kişi bulma şansı kabaca % 90’dır. Aynı odada en az 23 kişi bulunduğunda, bu sayı yalnızca % 50’ye düşmektedir.
Yıldırım düşündüğünden daha az çarpmaktadır: Amerika Birleşik Devletleri’nde, ömrü boyunca yıldırım çarpması ihtimali 3,000’de birdir. Ancak, bu saldırıdan tam olarak kurtulma şansı % 90’ın üzerindedir.
Kumar: New Jersey’deki bir kadın, zarlarını kaybetmeden sürekli olarak 154 kez atmıştır, bu da doğal olarak dünya rekorunu kırmıştır. Bunun olma olasılığı kabaca 5.6 milyarda birdir.
Silah kullanmak: Silahlı olmanın kişiyi silah şiddetinden daha iyi koruduğu düşünülüyorsa: Paris’teki Kasım 2015 saldırılarında kişi başına ölüm oranı, ABD’de herhangi bir ayda silahla öldürülen kişi başına düşen ortalama insan sayısından daha azdır.
Bir süpermodel ile çıkmak: Bir süper modelle çıkma şansı, poker oynarken bir floş elde etmekten yedi kat daha yüksektir, eskilerin 88.000’de bir kazanma ve ikincisi kabaca 650.000’de bir olma ihtimali yüksektir.
Kaynakça:
sciencing.com
mathsisfun.com
Yazar: Özlem Güvenç Ağaoğlu