 Matematikte Pisagor Teoremi olarak da bilinen teorem, Öklid geometrisinde, bir dik üçgenin üç kenarı arasındaki temel bir ilişkidir. Pisagor teoremi, hipotenüsün karesinin (dik açının karşısında yer alan, dik üçgenin en uzun kenarı) diğer iki kenarın karelerinin toplamına eşit olduğunu belirtir. Teorem, genellikle “Pisagor denklemi” olarak adlandırılan, a, b ve c kenarlarının uzunlukları ile ilgili bir denklem olarak yazılır:
Matematikte Pisagor Teoremi olarak da bilinen teorem, Öklid geometrisinde, bir dik üçgenin üç kenarı arasındaki temel bir ilişkidir. Pisagor teoremi, hipotenüsün karesinin (dik açının karşısında yer alan, dik üçgenin en uzun kenarı) diğer iki kenarın karelerinin toplamına eşit olduğunu belirtir. Teorem, genellikle “Pisagor denklemi” olarak adlandırılan, a, b ve c kenarlarının uzunlukları ile ilgili bir denklem olarak yazılır:
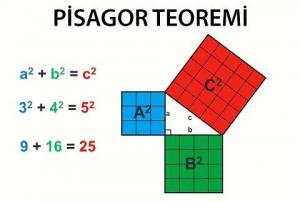
a2 + b2 = c2
Bu denklemde, a ve b üçgenin iki kenarını, c ise hipotenüsünü ifade etmektedir. Üçgenin her kenarından birer kare oluşturulduğunda, karelerin alanları, kare alan formülüne dayalı olarak a2, b2, c2 biçiminde sıralanırlar. Her üç karenin köşelerinin birleşimiyle meydana gelen dik üçgenin, dik açının bulunduğu köşesinden hipotenüsün bulunduğu karenin paralel kenarına indirilen dikmeyle de üçgende Öklid bağıntısı kurulmaktadır. Sayısız ispatı olan teoremin en basit kanıtlanma biçimi ise, bazı kaynaklarda filozof ve matematikçi Proklus’a ait olduğu belirtilen, Pisagor’un “yeniden düzenleme” yöntemidir.
Pisagor Teoremi, kendisinden çok daha önceki tarihlerde bulunmuş olduğu bilinse de, eski Yunanlı matematikçi Pisagor’un (M.Ö. 570 – M.Ö. 495) adıyla anılmaktadır. Mezopotamyalı, Hintli ve Çinli matematikçiler teoremi birbirlerinden bağımsız olarak keşfetmişler ve kanıtlamışlardır. Matematik teoremleri içinde üzerinde en çok durulan ve bazıları binlerce yıl öncesine dayanan geometrik ve cebirsel kanıtlar da dahil olmak üzere sayısız kez kanıtlanan Pisagor teoremi, mistik ya da entelektüel bir simge olarak matematiğin dışında da ilgi çekmiş, edebiyatta, tiyatro oyunlarında, müzikallerde, şarkılarda, pullarda ve karikatürlerde de yer almıştır.
Matematik tarihçisi Joran Friberg’e göre, kanıtlar, Pisagor teoreminin, Pisagor’un doğumundan bin yıl öncesine dayanan İlk Babil Hanedanlığı (M.Ö. 20. yüzyıldan M.Ö. 16. yüzyıla kadar) matematikçileri tarafından iyi bilindiğini göstermektedir. Gene, Dick Teresi, Babillilerin, Pisagor’dan en az on beş yüz yıl önce teoremi geliştirdiklerini belirtmektedir. Bartel Leendert van der Waerden (19031996), Pisagor üçlüsünün, Babilliler tarafından cebirsel olarak keşfedildiğini açıklamıştır.
M.Ö. 2000 ila 1786 yılları arasında yazılmış olan Mısır Orta Krallık dönemine ait Berlin Papirüsü 6619, çözümü Pisagor üçlüsü 6, 8, 10 olan bir problemi içermektedir. Büyük Hammurabi döneminde, M.Ö. 1790 ile M.Ö. 1750 yılları arasında yazılan Mezopotamya tableti Plimpton 322’de, Pisagor üçlüsü ile yakından ilişkili pek çok kayıt bulunmaktadır. Hindistan’da, M.Ö. 8. ve M.Ö. 5. yüzyıllar arasında, çeşitli olarak verilen Baudhayana Sulba Sutra yazmalarında, cebirsel olarak keşfedilmiş bir Pisagor üçlüsü listesi, Pisagor teoreminin anlatımı ve teoremin bir ikizkenar dik üçgen üzerindeki geometrik bir kanıtını içerir. Apastamba Sulba Sutra (M.Ö. 600) kayıtları ise, teoremin alan hesaplaması kullanılarak bulunmuş sayısal bir kanıtını içermektedir.
Eski Çin’in Zhoubi Suanjing metinleri (Gnomon’un Aritmetik Klasiği ve Cennetin Dairesel Yolları), 3, 4, 5 üçgeni için teoremi açıklar ve “Gougu teoremi” olarak adlandırır. Han Hanedanlığı döneminde (M.Ö. 202 – M.S. 220), Pisagor üçlüsü, Matematik Sanatı Üzerine Dokuz Bahis’te dik üçgenleri anlatan bölümde ele alınmıştır. Teoremi, ayrıca, Zhou Dükü’nün astronom ve matematikçisi Shang Gao’nun teoremi olarak adlandıran kaynaklar da vardır. Bu nedenle, bazı uzmanlar teoremin ilk kez Çin’de ortaya çıktığına inanmaktadır.
 Proklus’un, Öklid hakkındaki yorumlarına bakılırsa, Pisagor, üçlülerini oluşturmak için cebirsel yöntemler kullanmıştı. Ancak Proklus’un metinleri, M.S. 410 ve M.S. 485 arasında tarihleniyor. Thomas L. Heath’e (18611940) göre, Pisagor’un yaşadığı dönemden beş yüzyıl sonrasına kadar Yunan metinlerinde bu teoremin Pisagor’a ait olduğuna dair özel bir kayıt da bulunmamaktadır.
Proklus’un, Öklid hakkındaki yorumlarına bakılırsa, Pisagor, üçlülerini oluşturmak için cebirsel yöntemler kullanmıştı. Ancak Proklus’un metinleri, M.S. 410 ve M.S. 485 arasında tarihleniyor. Thomas L. Heath’e (18611940) göre, Pisagor’un yaşadığı dönemden beş yüzyıl sonrasına kadar Yunan metinlerinde bu teoremin Pisagor’a ait olduğuna dair özel bir kayıt da bulunmamaktadır.
Kaynakça:
– A.Posamentier,”The Pythagorean Theorem:The Story of Its Power and Beauty” Prometheus Books (2010).
– J.J.O’Connor, E.F.Robertson, “Pythagoras’s theorem in Babylonian mathematics”, School of Mathematics and Statistics, University of St. Andrews, (2017).
Yazar: Oben Güney Saraçoğlu
